Telegrams
A few days ago at work, a friend of mine came up with this problem. I call it the “telegram” problem: you get a string consisting of words run together without spaces, and figure out where spaces can go to separate out the words. For example, a famous misunderstanding:
parse_telegram("turkeytrotstowaterwhereistaskforcethirtyfourtheworldwonders") -- turkey trots to water where is task force thirty four the world wonders
I wrote a solution last night.
The dictionary
First things first, we’re going to need a dictionary of words. If you’re on a Mac or most Linux distros you already have one, at /usr/share/dict/words. If not, I recommend Googling for the OSPD, the Official Scrabble Player’s Dictionary.
The dictionary comes to us as a text file with one word per line. Mine, at least, contains a bunch of proper nouns, words with apostrophes, and single-letter words, which I filtered out (adding back “i” and “a,” the only two single-letter words that really exist).
We need to turn this into some kind of data structure we can easily query. Specifically, we want to quickly find out if there are any words that begin with a certain substring, for example, there are words that begin with “appl” but none that begin with “appq.” The data structure we’ll use for this is called a trie. It’s a tree with each node representing a letter, and the edges leading out of the node representing letters that could follow this one. So, for example, here’s a trie containing the words “an,” “ant,” “app,” “apple,” and “pear:”
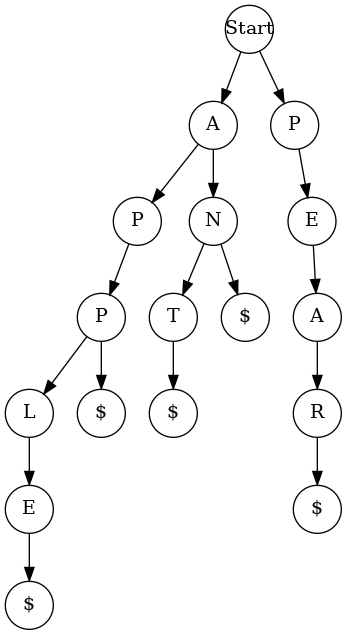
A “$” node represents the end of a word, so, if a node has a “$” as a child, that means that letter can complete a word (but doesn’t have to, if there are other children).
So, here’s a function that reads a dictionary file, filters out the words we don’t want, and inserts them into a trie:
function load_dictionary(filename) local dictionary = {} for line in io.lines(filename) do if line:match("^%l%l+$") then insert(dictionary, line .. "$") end end -- We're cutting all single-letter words, but -- two of them are real words insert(dictionary, "a$") insert(dictionary, "i$") return dictionary end
And here’s the corresponding insert function, to actually put them in the trie:
function insert(dictionary, word) local first = word:sub(1,1) dictionary[first] = dictionary[first] or {} if first ~= "$" then insert(dictionary[first], word:sub(2)) end end
Finding all possible words
The first step to my solution is to find all the possible words in the telegram, matched to their place in the string. So, for the telegram “hellothere” we will make a list of words like this:
hellothere he hell hello -ell ---lo ---lot ---loth ----other -----the -----there ------he ------her ------here -------ere --------re
(Your list may be slightly different using the OSPD instead of Ubuntu’s dictionary like I am.)
find_words takes a telegram and a trie and returns a list of {position, word} tuples for each word. The way it works is pretty straightforward: for each letter in the telegram, search the trie for words that start with that letter. So, we look for a “$” node under the first “h,” if we don’t find one we move down to “e” and then look for a “$” node, if we find one we insert “he” and then move down to “l,” and so on, until we reach a point where the current trie node doesn’t have a child for the next letter in the telegram. Then we stop and try again with the next starting letter.
function find_words(telegram, dictionary) local words = {} -- list of tuples, {start, word} for start = 1, #telegram do local current_index = start local current_letter = telegram:sub(start, start) local current_node = dictionary while current_node[ current_letter ] do current_node = current_node[ current_letter ] if current_node['$'] then table.insert(words, {start, telegram:sub(start, current_index)}) end current_index = current_index + 1 current_letter = telegram:sub(current_index, current_index) end end return words end
Culling the word list
Looking at our list of words, it should be clear that some of these can’t be part of any solution. For example, look at the word “lot” starting at position 4: any solution that contains “lot” must also contain a word that ends at position 3, as well as one that begins with position 7 (the left and right neighbors of “lot”). “Here” begins at 7, so we have a right neighbor, but nothing ends at 3, so, “lot” cannot be part of a solution.
We need to go through the list of tuples and remove any words that don’t have left and right neighbors. Of course, those words we remove might themselves be the neighbors of other words, meaning that removing them might leave those words without a neighbor. So we need to keep culling the list until there’s nothing left that can be removed.
We’ll make this fast by keeping a count of all the words that start and end at each position, and checking each word to ensure that that count is positive for each of them.
function cull_words(words, telegram_length) -- Map from start / end position, to word count local by_start = setmetatable( {}, {__index=function() return 0 end} ) local by_end = setmetatable( {}, {__index=function() return 0 end} ) -- Initialize these counts for _, w in ipairs(words) do local l = w[1] local r = w[1] + #(w[2]) - 1 by_start[l] = by_start[l] + 1 by_end[r] = by_end[r] + 1 end -- Loop until we run out of things to remove while true do local new_words = {} for i, w in ipairs(words) do local left = w[1] local right = w[1] + #(w[2]) - 1 local left_neighbor = (left == 1) or (by_end[left-1] > 0) local right_neighbor = (right == telegram_length) or (by_start[right+1] > 0) if left_neighbor and right_neighbor then table.insert(new_words, w) else by_start[left] = by_start[left] - 1 by_end[right] = by_end[right] - 1 end end if #new_words == #words then break end words = new_words end return words end
Enumerating the solutions
At this point, everything in our word list can be part of a solution. We can organize our words into a tree, like so:
iamatelegram i -a -am --ma --mate ---a ---ate ----telegram ------leg ---------ram
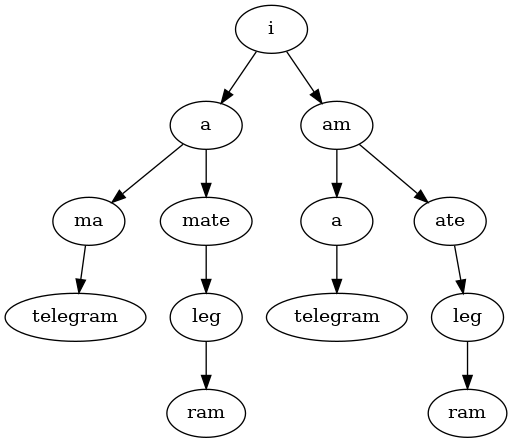
Here’s a simple function to do that:
function build_word_tree(words) local function find_by_start(start) local arr = {} for _,w in ipairs(words) do if w[1] == start then table.insert(arr, w[2]) end end return arr end local function tree_for_start(start) local tree = {} for _, w in ipairs(find_by_start(start)) do tree[w] = tree_for_start( start + #w ) end return tree end return tree_for_start(1) end
Now, every path through this tree is a possible solution. So, we simply do a depth-first traversal of the tree and list out all the paths:
function print_tree(word_tree) local strings = {} -- The paths through the tree local function dft(path, current_node) for word, children in pairs(current_node) do local new_path = path and path .. " " .. word or word if not next(children) then table.insert(strings, new_path) else dft(new_path, children) end end end dft(nil, word_tree) for _, s in ipairs(strings) do print(s) end end
Putting it together
Now that we have all the tools, we just run them all together:
function parse_telegram(telegram) local words = find_words(telegram, dictionary) local culled = cull_words(words, #telegram) local tree = build_word_tree(culled) print_tree(tree) end
Let’s test it out:
parse_telegram("turkeytrotstowaterwhereistaskforcethirtyfourtheworldwonders") -- turkey trots to water where is task force thirty four the world wonders
Again, you may get more possible solutions if you use a different dictionary.
Code, next steps
As always, the complete code is on Github. If you want to play with it, try messing around with the print_tree function: look for the path through the tree with the highest average word length (hint: the total word length will always be constant).